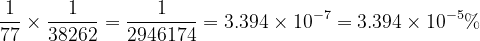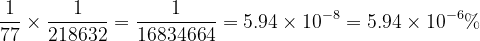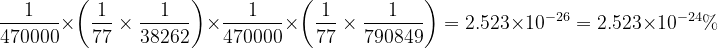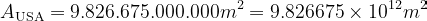Disclaimer1: Onderaan vanaf de Conclusie staan de resultaten + een reeks aan afbeeldingen.
Samenvatting
Wat is de kans dat het woord ‘Egypte’ het laatste woord is in het Boek Genesis, en het woord ‘Amen’ het laatste woord is in de Bijbel, in combinatie met het feit dat deze woorden respectievelijk precies 77 keer worden genoemd in Genesis en in de gehele King James Bijbel (KJV)? Hoe verhouden deze resultaten zich tot andere Bijbelversies? En hoe zou dit zich verhouden tot de kans om één enkel mosterdzaadje te selecteren uit een stapel mosterdzaadjes? De resultaten van linguïstische analyse en wiskundige waarschijnlijkheidsberekeningen benaderen deze kansen respectievelijk als het vinden van een mosterdzaadje op een oppervlakte van tussen de 0,02 m² en 0,44 m², en als het selecteren van een mosterdzaadje uit een stapel die de landoppervlakte van de VS bedekt tot een hoogte van 10 km tot 50 km!
Inleiding
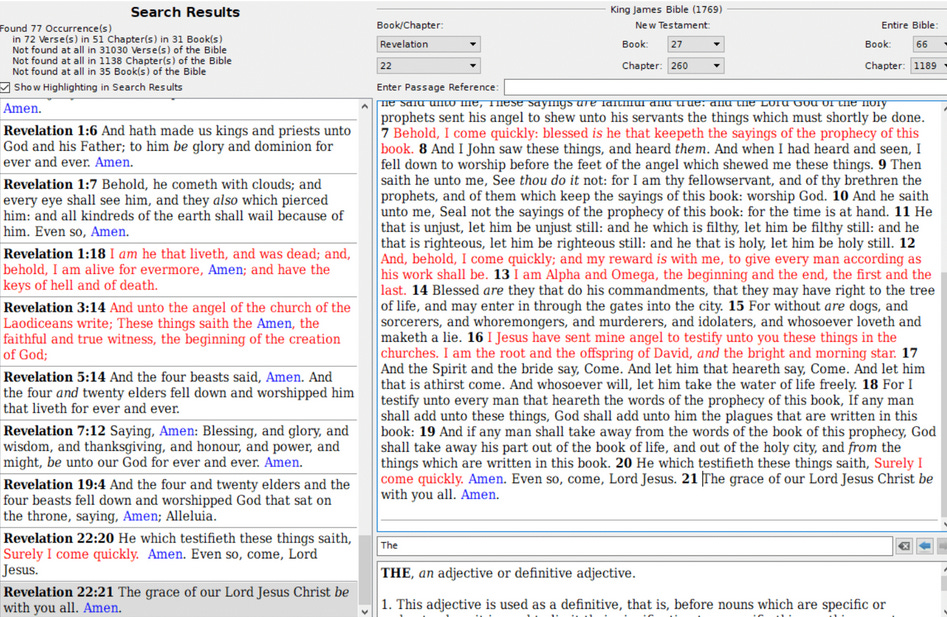
Ten eerste wordt de King James Pure Bible Search (KJPBS) softwaretool gebruikt om het voorkomen van individuele woorden te analyseren. Deze tool biedt uiterst nuttige gegevens over het aantal woorden in afzonderlijke boeken, bijvoorbeeld het Boek Genesis (heeft 38.262 woorden), en voor de gehele Bijbel (heeft 790.849 woorden). Het is ook mogelijk om een oneindig aantal zoekopties uit te voeren voor individuele woorden en combinaties van woorden binnen afzonderlijke boeken van de Bijbel, zowel in het Oude als in het Nieuwe Testament. In dit geval, wanneer er wordt gezocht naar het woord ‘Egypt’ dat alleen in het Boek Genesis voorkomt, zijn er 77 overeenkomsten (zie onderstaande Figuur).
Egypt
77 resultaten in het eerste boek Genesis
‘Egypt’ is het laatste woord van het boek Genesis
AMEN
Het woord 'Amen’ (met een Hoofdletter) wordt 77 keer vermeld in de hele Bijbel.
‘Amen’ is het laatste woord van de Bijbel en het laatste Boek
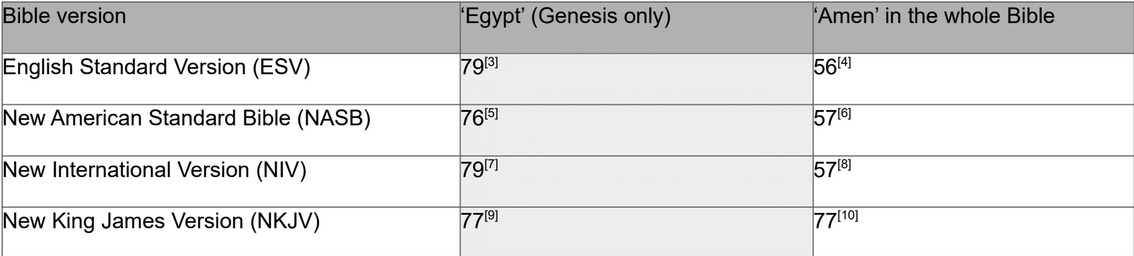
Hoe verhouden andere Bijbelversies zich?
Met behulp van de online zoektool van Blue Letter Bible kunnen dezelfde zoekopdrachten worden uitgevoerd in andere Bijbelversies. Uit de resultaten blijkt duidelijk dat alleen de New King James Version (NKJV) overeenkomt met de zoekresultaten van de King James Version (KJV).
Methode
Er zijn uiteraard verschillende manieren om de waarschijnlijkheid van het voorkomen van bepaalde woorden in een tekst te kwantificeren. In deze studie zijn twee verschillende benaderingen gehanteerd. Ten eerste is er een vereenvoudigde wiskundige analyse van waarschijnlijkheid toegepast, een techniek die het gemakkelijkst kan worden uitgelegd met behulp van dobbelstenen. Dit is een basisbenadering om te analyseren hoe vaak een bepaald woord, uit alle mogelijke opties in het relevante vocabulaire, gekozen zou kunnen worden. Hiervoor zijn twee versies geselecteerd: Webster’s 1828 Dictionary2 en de Oxford English Dictionary3.
De tweede analyse maakt gebruik van de frequentie van woorden door middel van de ‘N-gram generator’4. Met deze online software kan worden gezocht naar een zin die uit 2 woorden bestaat (bigram (2)) tot aan een zin die uit 5 woorden bestaat (N-gram (5)). De resultaten kunnen worden gerangschikt in de top 10 tot de top 1000, gesorteerd op ‘Frequentie/Waarschijnlijkheid/Sterkte’, en een ‘minimalefrequentie’ van 1 tot 100 kan worden ingesteld. Er is ook een handige link naar de tekst van de KJV Bijbel5 waarmee relevante tekst kan worden gekopieerd en geplakt in de zoekmachine.
Beginnend met de benadering van wiskundige waarschijnlijkheden, wordt waarschijnlijkheid eerst gedefinieerd als ‘het deel van de keren dat een uitkomst naar verwachting zal plaatsvinden’. Wanneer een uitkomst onvermijdelijk is, kan dit worden uitgedrukt in breukvorm, digitaal en als percentage (%), zoals volgt.
In het geval van een dobbelsteen, met één zijde kop en de andere munt, is de kans om kop te krijgen als volgt te berekenen:
Hoeveel zijden van de dobbelsteen zouden nodig zijn voor deze uitkomst? De breuk moet worden 'omgekeerd' om het resultaat van 2 ÷ 1 = 2 zijden te verkrijgen.
De volgende twee regels worden gebruikt voor het combineren van waarschijnlijkheden (Wiskundige Regels 1 en 2).
Regel 1: De vermenigvuldigingsregel voor waarschijnlijkheden
Als een aantal uitkomsten ONAFHANKELIJK van elkaar optreden, wordt de kans dat ze allemaal SAMEN plaatsvinden berekend door hun individuele waarschijnlijkheden met elkaar te VERMENIGVULDIGEN.
Bijvoorbeeld, als je 3 dobbelstenen gooit, wat is dan de kans om op elke dobbelsteen een 4 te gooien? De kans op een 4 op één dobbelsteen is 1 ÷ 6. Dus de kans om op alle dobbelstenen een 4 te gooien is 0,4629% .
Regel 2: De optelregel voor waarschijnlijkheden
Als een aantal ALTERNATIEVE uitkomsten WEDERZIJDS UITSLUITEND zijn, wordt de kans om EEN VAN deze uitkomsten te krijgen berekend door hun individuele waarschijnlijkheden bij elkaar op te TELLEN.
Bijvoorbeeld, wat is de kans om een 4 OF een 5 te gooien bij ÉÉN worp met een dobbelsteen? De kans op een 4 is 1 ÷ 6, en de kans op een 5 is ook 1 ÷ 6. De gecombineerde kans is dus 33,33% (zie Wiskundig Resultaat 2).
Stellingen
De kans dat ‘Egypt’ het laatste woord is
‘Egypt’ is het laatste woord in het Boek Genesis.
Volgens Webster’s 3rd New International Dictionary zijn er 470.000 mogelijke woorden.
De kans dat ‘Egypt’ het laatste woord is, wordt als volgt berekend:
Vergelijking 1
Om één goud mosterdzaadje te vinden, zou je 470.000 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 470.001 zaadjes zou vereisen.
Volgens de 2e editie van de Oxford English Dictionary zijn er 171.476 woorden in huidig gebruik en 47.156 ‘verouderde’ woorden. Dit maakt een totaal van 218.632 woorden.
De kans dat ‘Egypt’ het laatste woord is, wordt als volgt berekend:
Vergelijking 2
Om één gouden mosterdzaadje goud te vinden, zou je 218.632 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 218.633 zaadjes zou vereisen.
De kans dat ‘Egypt’ & ‘Amen’ tussen de 1 en 100 keer wordt genoemd
‘Egypt’ wordt 77 keer genoemd in het Boek Genesis, en ‘Amen’ wordt 77 keer genoemd in de hele Bijbel.
Laten we eerst de kans berekenen dat ‘Egypt’ tussen de 1 en 100 keer wordt genoemd in het Boek Genesis. Hiervoor kan Wiskundige Regel 2 worden toegepast:
Vergelijking 3
Met behulp van de online ‘Sigma/summation calculator’6 komt het eindresultaat uit op 5,187377517639621, afgerond op 5,187.
Op dezelfde manier is de kans dat ‘Amen’ tussen de 1 en 100 keer in de hele Bijbel wordt genoemd ook 5,187.
De gecombineerde kans, gebruikmakend van Wiskundig Resultaat 1 aangezien deze uitkomsten onafhankelijk zijn, is als volgt:
Vergelijking 4
De gecombineerde kans dat zowel ‘Egypt’ als ‘Amen’ tussen de 1 en 100 keer voorkomen in respectievelijk het Boek Genesis en de hele Bijbel, is ongeveer 0,02% (3,717% ÷ 200 opties, aangezien 77 één van de 100 mogelijke opties is, en er twee woorden zijn).
De kans hoe frequent ‘Egypt’ voorkomt en geplaatst is
‘Egypt’ wordt 77 keer genoemd in het Boek Genesis en het totale aantal woorden in het Boek Genesis is 38.262.
Aangezien deze uitkomsten onafhankelijk van elkaar zijn, wordt Wiskundige Regel 1 toegepast.
De kans dat deze 77 vermeldingen van ‘Egypt’ in het Boek Genesis voorkomen, wordt als volgt berekend.
Vergelijking 5
Om één mosterdzaadje goud te verven, zou je 2.946.174 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 2.946.175 zaadjes zou vereisen.
Opmerkelijk is ook dat ‘Egypt’ het ENIGE woord is van de 2.509 unieke woorden in Genesis dat precies 77 keer wordt genoemd.
Aangezien deze uitkomsten onafhankelijk van elkaar zijn, wordt opnieuw Wiskundige Regel 1 toegepast.
De kans dat dit gebeurt, wordt als volgt berekend
Vergelijking 6
Om één mosterdzaadje goud te verven, zou je 193.193 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 193.194 zaadjes zou vereisen.
De kans dat ‘Egypt’ 77x voorkomt EN het laatste woord is van het boek
‘Egypt’ is het enige woord dat 77 keer wordt genoemd in Genesis, is tevens het laatste woord van dit boek.
Aangezien deze uitkomsten onafhankelijk van elkaar zijn, wordt Wiskundige Regel 1 toegepast.
Op basis van de waarden uit Webster’s Engelse woordenboek hebben we de volgende waarschijnlijkheden:
Vergelijking 7
Om één goud mosterdzaadje goud te vinden, zou je 36.190.000 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 36.190.001 zaadjes zou vereisen.
Op basis van de waarden uit de Oxford English Dictionary hebben we de volgende waarschijnlijkheden:
Vergelijking 8
Om één goud mosterdzaadje te vinden, zou je 16.834.664 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 16.834.665 zaadjes zou vereisen.
‘Egypt’ als een vermenigvuldigde waarschijnlijkheid
Met behulp van de ‘N-gramgenerator’ en het wijzigen van de standaardinstellingen naar een trigram (3) woordinstelling, worden de resultaten verkregen in onderstaande:
Onderstaande tabel toont de resultaten, georganiseerd in zinnen van drie woorden. Hier laat de Wiskundige Regel 1 zien dat de vermenigvuldigde waarschijnlijkheid van de 48 keer dat het woord ‘Egypt’ voorkomt in de betreffende drie woorden een totaal is van 0,000011115 = 1,11115 x 10-5. Het omgekeerde is 90.000.
Resultaat 1
Als u de standaardinstellingen van de ‘N-gramgenerator’ wijzigt naar de maximale N-gram woordinstelling, worden de volgende resultaten verkregen:
Onderstaande toont de resultaten, georganiseerd in zinnen van vijf woorden.
Hier laat de Wiskundige Regel 1 zien dat de vermenigvuldigde waarschijnlijkheid van 64 keer voorkomen van het woord ‘Egypt’ in de vijf betreffende woorden een totaal is van 0,0002 = 2,0 x 10-4.
Het omgekeerde hiervan is 5.000
Resultaat 2
De kans dat ‘Amen’ het laatste woord is
‘Amen’ is het laatste woord in het Boek Openbaring.
Volgens Webster’s 3rd New International Dictionary zijn er 470.000 mogelijke woorden.
De kans dat ‘Amen’ het laatste woord is, wordt als volgt berekend:
Vergelijking 9
Om één goud mosterdzaadje te vinden, zou je 470.000 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 470.001 zaadjes zou vereisen.
Volgens de 2e editie van de Oxford English Dictionary zijn er in totaal 218.632 woorden. De kans dat ‘Amen’ het laatste woord is, wordt als volgt berekend:
Vergelijking 10
Om één goud mosterdzaadje te vinden, zou je 218.632 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 218.633 zaadjes zou vereisen.
De kans dat ‘Amen’ 77x voorkomt in de hele Bijbel
‘Amen’ wordt 77 keer genoemd in de hele Bijbel.
Het totale aantal woorden in de Bijbel is 790.849.
Aangezien deze uitkomsten onafhankelijk van elkaar zijn, wordt de Wiskundige Regel 1 toegepast.
Wat is dus de kans dat de 77 vermeldingen van ‘Amen’ in de hele Bijbel voorkomen?
Vergelijking 11
Om één goud mosterdzaadje te vinden, zou je 60.895.373 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 60.895.374 zaadjes zou vereisen.
‘Amen’ als een vermenigvuldigde waarschijnlijkheid
Als u de standaardinstellingen van de ‘N-gramgenerator’ wijzigt naar een trigram (3) woordinstelling, worden de volgende resultaten verkregen.
Onderstaande toont de resultaten, georganiseerd in zinnen van 3 woorden tot 1000 keer voorkomend. Hier is de kans op het 77 keer te vinden van ‘Amen’ in feite verwaarloosbaar.
Als u de standaardinstellingen wijzigt naar een woordinstelling van N-gram (5), worden de resultaten verkregen in onderstaande tabel. Als u dit herschikt in termen van het woord 'Amen', is dit in deze instelling van 5 woorden nummer 875 van 1000 in 'Frequentie' ' maar met een waarschijnlijkheid van feitelijk nul!
Le Moment Suprême
Wat is de kans dat zowel ‘Egypt’ als ‘Amen’ de laatste woorden zijn van respectievelijk het eerste boek (Genesis) en het laatste boek (Openbaring), terwijl ze BEIDE precies 77 keer worden genoemd? Aangezien deze uitkomsten onafhankelijk van elkaar zijn, wordt Wiskundige Regel 1 toegepast.
Het is belangrijk op te merken dat de resultaten van de ‘N-gram generator’ niet bruikbaar zijn, aangezien de resultaten voor het woord ‘Amen’ praktisch nihil zijn.
Kansen volgens de Webster’s 1828 Dictionary
Op basis van Webster’s 1828 Dictionary wordt de kans als volgt berekend: Vergelijking (1) x Vergelijking (5) x Vergelijking (9) x Vergelijking (11) Het omgekeerde hiervan is 3,964 x 10^25
Resultaat 3
Dit is een gigantisch getal! Om één goud mosterdzaadje te vinden, zou je 396.400.000.000.000.000.000.000.000 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 396.400.000.000.000.000.000.000.001 zaadjes zou vereisen!
Kansen volgens de Oxford English Dictionary
Op basis van Oxford English Dictionary wordt de kans als volgt berekend:
Vergelijking (2) x Vergelijking (5) x Vergelijking (10) x Vergelijking (11) Het omgekeerde hiervan levert opnieuw een gigantisch getal op: 8,576 x 10^24!
Resultaat 4
Om één goud mosterdzaadje te vinden, zou je 8.576.000.000.000.000.000.000.000 andere mosterdzaadjes in een pot moeten hebben, wat een totaal van 8.576.000.000.000.000.000.000.001 zaadjes zou vereisen!
Berekeningen van de 'Orde van grootte'
De formule ontleden
Gezien de diameter van een mosterdzaadje (dMustardseed) 2,5 mm7 is, dan berekenen we wat de straal (rMustardseed) is:
Vergelijking 12
Dan is de oppervlakte (Amosterdzaad), aangenomen dat de vorm van een zaadje een perfecte cirkel is:
Dus, hoeveel mosterdzaadjes (N) zouden nodig zijn om de gehele VS te bedekken?
Vergelijking 15
De formule toepassen
Ten eerste: door de eerdere resultaten (1) en (2) te nemen, wat zijn de equivalente oppervlakten (A1) en (A2)? (zie onderaan resultaten 5 en 6)
Ten tweede: bij het analyseren van de eerdere resultaten (3) en (4), hoeveel lagen (L1) en (L2) kunnen worden geproduceerd en wat zijn de geschatte hoogten (H1) en (H2) van deze lagen? (zie onderaan resultaten 7 en 8)
Resultaat 5: Voor 90.000 zaden
Ten eerste zouden 90.000 (9,0 x 10⁴) zaden het volgende gebied bestrijken (0.44181m²):
Resultaat 5
Resultaat 6: Voor 5.000 zaden
Op dezelfde manier: 5.000 (5,0 x 10³) zaden zouden het volgende gebied bedekken (0.024545m²) ;
Resultaat 6
Resultaat 7: Voor 3,964 x 10 tot de macht 25 zaden
Dit aantal zaden zou 19.800.000 lagen opleveren die de hele VS bestrijken! Op een hoogte van 49,5 km of 30,75 mijl!
Resultaat 8: Voor 8.576 x 10 tot de macht 24 zaden
Dit aantal zaden zou 4.284.000 lagen opleveren die de hele VS bestrijken! Op een hoogte van 10,7 km of 6,64 mijl!
Conclusie
Met de bovenstaande vergelijking komen we tot de verbijsterende conclusie dat de kans op toeval zo verwaarloosbaar klein is, dat het letterlijk de gehele Verenigde Staten zou bedekken met een zee van mosterdzaadjes. Deze laag zou niet alleen het land bedekken, maar ook elke bergketen bedelven onder een deken van zaadjes, variërend van 10 tot 49 kilometer hoog. En slechts één van deze miljarden zaadjes zou de gouden winnaar zijn.
Stel je voor dat je een AI of robot de opdracht geeft om een Bijbel te schrijven, met hetzelfde aantal woorden, hoofdstukken en boeken. Ongeacht de specifieke woorden die gebruikt worden, is er slechts 1 kans op 396.400.000.000.000.000.000.000.000 dat deze tekst identiek zou zijn. Om een idee te geven van deze astronomischekans: als je elk zaadje per seconde zou tellen, zou het 125,6 miljard jaar duren om ze allemaal te tellen—om maar een illustratie te geven uit het nihilisme en de wilde theorieën die worden verspreid zonder enige vorm van bewijs: dat is 111,6 miljard jaar langer dan de “geschatte leeftijd” van het universum.
Hoewel men zou verwachten dat andere Bijbels, vooral de NKJV, soms dezelfde resultaten zouden repliceren als de KJV, is dit verre van gegarandeerd. Hoewel alle Bijbels in het Engels zijn vertaald uit schijnbaar dezelfde bronnen, zouden de berekende waarschijnlijkheden NIET gelijk zijn voor deze andere vertalingen, simpelweg omdat het aantal woorden in de KJV verschilt van de rest, en zelfs van elkaar!
Wat zijn dan de kansen dat zowel 'Egypt' als 'Amen' de laatste woorden zijn van zowel het eerste boek (Genesis) als het laatste boek (Openbaring) in de KJV, waarbij BEIDE precies 77 keer worden genoemd? Vergeleken met de kans om één mosterdzaadje te trekken uit een gigantische stapel, zijn deze kansen gelijk aan het kiezen van één mosterdzaadje uit een oppervlak bedekt met een laag mosterdzaadjes tussen 0,02 m² en 0,44 m². Maar als we wiskundige waarschijnlijkheden gebruiken, gebaseerd op de selectie van slechts één woord uit de Webster's en Oxford Dictionaries, dan komt dit neer op de kans om één mosterdzaadje te kiezen uit een laag die de gehele VS bedekt, met een diepte/hoogte variërend van 10 tot 50 km!
